Part III. C.: Interlude. The F.E.D. Psychohistorical-Dialectical 'Meta-Equation' of Human-Social Formation(s) 'Meta-Evolution' Series.
Modeling the Systematic Dialectic of
‘‘‘The Basic Operations
of Arithmetic’’’ using CQ_ --
Systematically Presented via a 5-Symbol
Expression.
Dear Reader,
Below is the third and final entry on the three simpler examples of systematic 'dialectical meta-models', presented as an interlude, before concluding the series on the F.E.D. Psychohistorical-Dialectical 'Meta-Equation' of Human-Social Formation(s) 'Meta-Evolution', with the problematics of the nation-state social formation, and with its 'meta-model'-predicted successor-formations.
Enjoy!
Regards,
Miguel
Introduction. This ‘meta-model’ is more “Complex” [pun intended] than the ‘meta-models’ of “TV-Series”,
and of ‘Modern Computerware’, presented earlier in this sub-series, in particular, because it
requires some “domain-expertise” -- or, at least, some “domain familiarity” --
with respect to the domain of the so-called “Complex Numbers”, the set standardly denoted by the symbol C.
The ‘axioms-system’ of the arithmetic of the C numbers, which we denote by C, is the 6th system of arithmetic in the following standard order of standard arithmetics, with our light-spectrum ordinal color-coding added --
The ‘axioms-system’ of the arithmetic of the C numbers, which we denote by C, is the 6th system of arithmetic in the following standard order of standard arithmetics, with our light-spectrum ordinal color-coding added --
N, W, Z, Q, R,
C,
-- for the “Natural”, “Whole”, “Integer”, “Rational”, “Real”, and “Complex” arithmetics, respectively.
About the ‘Goedelian Dialectic’ of these systems, see: http://www.dialectics.info/dialectics/Vignettes.html, Vignette #4.
-- for the “Natural”, “Whole”, “Integer”, “Rational”, “Real”, and “Complex” arithmetics, respectively.
About the ‘Goedelian Dialectic’ of these systems, see: http://www.dialectics.info/dialectics/Vignettes.html, Vignette #4.
We will, in this blog-entry, use the Complex-Numbers-subsuming version of the F.E.D. ‘first dialectical algebra’ to construct, and to “solve”, a “heuristic”, ‘intensional’ [‘connotational’],‘intuitional’ ‘meta-model’ of a systematic presentation of the domain of “the basic operations of arithmetic” -- encompassing both its ‘‘‘verse’’’ [e.g., addition, multiplication, exponentiation] and its “inverse” [e.g., subtraction, division, root-extraction] operations, jointly, via qs with C subscripts, i.e., with “Complex-number” subscripts, which we also reference as Cqs.
The ‘meta-models’ that we usually narrate here are constructed by interpreting the generic NQ_ version of the F.E.D. ‘first dialectical algebra’ [ see E.D.Brief # 5 and its Preface ], or, at most-advanced, by interpreting the generic WQ_ version of that algebra [ see E.D.Brief #6 and its Preface ], with the subscripts of the Nq or Wq ‘meta-numerals’ drawn from the number-space N = { 1, 2, 3, ... }, or from the number-space
W = { 0, 1, 2,
3, ... }, respectively.
This time, the subscripts of the Cqs will be drawn from the standard number-space --
C = { R + Ri },
-- wherein R denotes the space of the standard so-called “Real” numbers, and where the i unit stands for so-called "imaginary" unity, the positive square root of -1.
FYI: The generic Complex number is often expressed as a + bi, with a an element of R, and also with b an element of R, or as z = x + yi, with x an element of R, and also with y an element of R.
That is, we will be constructing our example model using the generic CQ_ version of the F.E.D. ‘first dialectical algebra’.
We use the CQ_ language
this time, as it allows us to present both ‘‘‘verse’’’ & ‘‘‘reverse’’’ operations in a single model.
Herein we mean, by the word, ‘‘‘systematic’’’ in the phrase ‘‘‘systematic presentation’’’, a presentation of the major kinds of “entities” that
exist in this 'Human-Phenomic', 'Meme-etic' domain, the domain of the basic operations of arithmetic -- by
means of categories that classify those entities by their “kinds”, i.e., as ‘‘‘[ideo-]ontology’’’, or as “kinds of [idea-]things, or "meme-things"” -- and in strict order of rising complexity, starting from
the simplest category, and moving, step-by-step, from lesser to greater, i.e.,
more inclusive, complexity, until we reach the most complex/inclusive extant
category of this domain, or for the purposes of this example.
The model that we build will
describe these categories in that strict, systematic order of rising
operational complexity / inclusivity.
This will be, once again,
like the previous two “interlude” models, a “snapshot” model, a “synchronic”
model that takes the contemporary slice of time -- or at any rate, a
recent-past slice of time -- and algorithmically generates descriptions of
categories for entities that presently exist, or that might possibly presently
exist, for the model’s domain, in their systematic order of inclusivity, as
described above.
Our model here will not be a “chronology”
model, or “diachronic”
model, like the previous, major model, narrated in this series, in which the
units of earlier categories are
described as actually, e.g., physically, constructing,
through their activity
as “causal agents”, i.e., as “subjects”, the units of later categories, categories whose units did not exist until that
construction took place.
That is, it will not be a model of a ‘self-advancing’ historical progression of ontology, with each historical epoch containing both old ontology, inherited from past historical epochs, plus new ontology, ontology that had never appeared before -- in past historical epochs -- until the later epoch in question, plus ‘hybrid categories’, combining / synthesizing the old with the new.
That is, it will not be a model of a ‘self-advancing’ historical progression of ontology, with each historical epoch containing both old ontology, inherited from past historical epochs, plus new ontology, ontology that had never appeared before -- in past historical epochs -- until the later epoch in question, plus ‘hybrid categories’, combining / synthesizing the old with the new.
We will apply a documented, standard
procedure
to “solve” this ‘‘‘algebratric’’’ model -- to determine what actual category
each of these generated category-descriptions refers to, and to determine
which, if any, of these category-descriptions describe “empty categories”,
i.e., represent ‘combinatorially’ possible entities that actually do
not exist "within" this domain -- at least not presently.
To get started, we must
determine the starting-point -- the point-of-departure -- for our systematic model.
This starting category will
be the seed of our whole progression of generated category-descriptions,
influencing every category that follows, as the “controlling source”, and as
the “ever-present origin”, of all that follows from it.
The rule for getting started
is to ask oneself “¿What is
the least complex kind
of thing, the simplest
kind of thing, the least inclusive kind of thing, which inheres in this domain?” -- in our case, in the domain of ‘basic arithmetic
operations’ -- and to then find the answer to that question, based upon one’s
prior knowledge of, or familiarity with, this domain.
The answer to this starting
question that we will pursue in this example is the following: The ‘‘‘verse’’’
operations of “Additions”,
and its “inverse operations”, or ‘‘‘reverse
operations’’’, or “Subtractions”,
are the simplest ancestors, the ultimate units, of basic arithmetical
operations, ingredient in every one of the more complex operations of that
domain.
A letter that the spelled
names of these two kinds of operations have in common is “t”.
Therefore, we shall
name/symbolize our starter category as Ct, or as Cqt, denoting the “Complex” combination of the “Additions” sub-category of elementary Real arithmetic basic operations, with the sub-category
of “Subtractions”,
and identifying that combination of specific
sub-categories with the generic
first category
symbol of our generic
category-arithmetic model, namely, with the symbol --
Cq[1 + 1i],
in an “identification”, an “interpretation”, or an “assignment” [ ‘[---)’ ] that we indicate by writing:
Ct = Cqt = Cq[A + Si] [---) Cq[1 + i].
Cq[1 + 1i],
in an “identification”, an “interpretation”, or an “assignment” [ ‘[---)’ ] that we indicate by writing:
Ct = Cqt = Cq[A + Si] [---) Cq[1 + i].
Our model then, will take the
form of an “interpeted”, specific
equation, assigned to the generic
equation, like this --
C)-|-(s = Ct2^s = ( Cq[A + Si] )2^s [---)
C|-|-|h = Ca2^h = [ Cq[1 + 1i] ]2^h
C|-|-|h = Ca2^h = [ Cq[1 + 1i] ]2^h
-- with the variable s indicating the step in our systematic
method of presentation that
the ‘accumulation of categories’, denoted by C)-|-(s, represents.
We will not, here, further recount the [Marxian] method of systematic discovery that was used to arrive at the starting category of this systematic presentation.
For more regarding that method of discovery, see Marx, Grundrisse, Penguin Books [London: 1972], pp. 100-101.
We will not, here, further recount the [Marxian] method of systematic discovery that was used to arrive at the starting category of this systematic presentation.
For more regarding that method of discovery, see Marx, Grundrisse, Penguin Books [London: 1972], pp. 100-101.
Stage 0. Our
initial step -- step s = 0 -- contains only our starting category --
Ct = Cqt = q[A + Si] --
C)-|-(0 = Ct2^0
= Ct1 = Ct =
Cq[A + Si] [---) Cq[1 + 1i]
Cq[A + Si] [---) Cq[1 + 1i]
-- because 2 “raised” to the power 0
-- 20 -- is just 1,
and because Ct “raised” to the power 1 is just Ct.
and because Ct “raised” to the power 1 is just Ct.
Stage 1. It is
when we get to the next step
after step s = 0, namely, to step s = 1, that our ‘meta-equation meta-model’ gives us back something
initially “unknown” -- and, therefore, something ‘‘‘algebraical’’’, not merely
something ‘‘‘arithmetical’’’:
something to “solve-for” --
)-|-(1 = Ct2^1
= Ct2 = Ct x Ct =
Cq[A + Si] x Cq[A + Si] =
Cq[A + Si] x Cq[A + Si] =
Cq[A + Si] + Cq[AA + SSi] = Cqt + Cqtt
-- because 2 “raised” to the power 1
-- 21 -- is just 2, and because
our rule for multiplying a generic category, call it --
Cq[X + Yi] = CqZ = CZ
-- “by”, or “into”, itself, is, for subscripts X and Y denoting sub-category symbols, and for subscript Z denoting a category-symbol, simply --
Cq[X + Yi] = CqZ = CZ
-- “by”, or “into”, itself, is, for subscripts X and Y denoting sub-category symbols, and for subscript Z denoting a category-symbol, simply --
Cq[X + Yi] x
Cq[X + Yi] =
Cq[X + Yi] + Cq[XX + YYi] = CZ + CqZZ
Cq[X + Yi] + Cq[XX + YYi] = CZ + CqZZ
-- and for x and y denoting “Real” numbers --
Cq[x + yi] x Cq[x + yi] =
Cq[x + yi] + Cq[(x + x) + (y + y)i] =
Cq[1x + 1yi] + Cq[2x + 2yi].
Cq[x + yi] + Cq[(x + x) + (y + y)i] =
Cq[1x + 1yi] + Cq[2x + 2yi].
Note again: Herein, Cq denotes the generic category ‘qualifier’ with “Complex” subscripts.
The subscripts that come after it are specific category descriptors.
¿But how do we discover what the resulting, initially
“unknown”, or ''algebraical'', ‘category-description’, here Cqtt, means?
Well, the generic rule to “solve-for” the categorial meaning of such symbols is that, if we know what is meant by category CqZ = CZ, then the symbol CqZZ describes a category each of whose units is a ‘CZ OF CZs’, that is, a category for a different kind of units, called ‘meta-CZs’, each such unit being made up out of a multiplicity of those units of which the category of the CZs is made up.
To be specific with this rule, in our
example-model, CqZZ specifies a “Complex” of two sub-categories.
Each of the units of the first sub-category,
the sub-category of the ‘‘‘verse’’’ operations, must be an ‘Addition OF
Additions’ that is, must be a ‘meta-Addition’, such that each ‘meta-Addition’ is made up out of a multiplicity
of “mere” Additions.
Each of the units of the second
sub-category, the sub-category of the ‘‘‘inverse’’’ operations, must be a ‘Subtraction OF
Subtractions’, that is, must be a ‘meta-Subtraction’, such that each such ‘meta-Subtraction’ is made up out of a multiplicity
of “mere” Subtractions.
Our
experiences of / "in" the domain of 'the basic operations of
arithmetic' suggest that such operations do “presently” exist in the
domain of “Real” arithmetic.
“Multiplication” is a basic arithmetical operation that is “made up
out of multiple [repeated] additions”, viz. --
4 x 5 = 5 + 5 +
5 + 5 =
4 + 4 + 4 + 4 + 4 = 5 x 4 = 20
-- a sum of four fives, or a
sum of five fours: either order
will do [a characteristic called “commutativity of addition”]!
In a partial reverse
likeness, “division” is a
basic arithmetical operation that is “made up out of multiple [repeated]
subtractions”, viz., 5 "goes ["evenly", i.e., with 0 remainder] into 20" 4 times; 4 "goes ["evenly"] into 20" 5 times --
20 ÷ 5 = 4;
20 - 5 - 5 - 5 - 5 = 0 = 20 - 4 - 4 - 4 - 4 - 4;
20 ÷ 4 = 5
20 - 5 - 5 - 5 - 5 = 0 = 20 - 4 - 4 - 4 - 4 - 4;
20 ÷ 4 = 5
-- to see how many fours
there are in twenty [not the same as how many twenties there are in four]; how many “times”
four “goes ["evenly"] in to” twenty, or to see how many fives there are in twenty, [not the same as how many twenties there are in five]; how
many “times” five “goes ["evenly"] in to” twenty:
but, in this case, either order will not do!
A letter that the spelled names of these two kinds of operations have in common is “n”.
Therefore, we shall name/symbolize our second category as Cn, or asCqn, denoting the “Complex” combination of the “muLtiplications” sub-category of elementary Real arithmetic basic operations, with the sub-category of “diVisions”, and identifying that combination of specific sub-categories with the generic second category symbol of our generic category-arithmetic model, namely, with the generic category-symbol
Cq[2 + 2i].
We may “assert” our solution as follows:
Cqtt =
Cqn = Cn = Cq[L + Vi]
= Cq[AA + SSi] [---) Cq[2 + 2i].
= Cq[AA + SSi] [---) Cq[2 + 2i].
Again, what is dialectical about the
relationship between Ct and Ct2, or Ct x
Ct, or Ct of Ct, or Ct(Ct), the
relationship of what we call ‘meta-unit-ization’, or ‘meta-«monad»-ization’, between Ct and its already presently existing, ‘supplementary other’, Cn, is that this relationship is a synchronic
double-«aufheben»
relationship.
That is, each single “unit”
of the “muLtiplications” sub-category of category Cn, i.e., each typical individual “multiplication” operation, is a negation,
and also a preservation,
by way of also being an elevation
to the / forming
the “higher” / more inclusive “muLtiplications” sub-category / level / scale, of a whole [sub-]group of units
of the “Additions”
sub-category / level / scale of the Ct category.
Likewise, each single “unit”
of the “diVisions” sub-category of category Cn, i.e., each typical individual “division” operation, is a negation,
and also a preservation,
by way of also being an elevation
to the / forming
the “higher” / more inclusive “diVisions” sub-category / level / scale, of a whole [sub-]group of units
of the “Subtractions”
sub-category / level / scale of the Ct category.
So, our full solution to the step s = 1 equation of our model is --
C)-|-(1 =
Ct + Cn =
Additions & Subtractions + MuLtiplications & DiVisions
Additions & Subtractions + MuLtiplications & DiVisions
[---) Cq[1 + 1i] + Cq[2 + 2i].
If this ‘meta-model’ is working
right, Additions & Subtractions is
the simplest category of
the domain of ‘basic arithmetical operations’; MuLtiplications & DiVisions is the next more complex category of
that domain.
Stage 2. ¿What additional ‘category-specifications’
do we generate in our next step, step s = 2, that need “solving-for”?
Let’s find out --
C)-|-(2 = Ct2^2 =
Ct4 =
( Ct2 )2 =
( Ct + Cn )2 =
( Ct + Cn ) x ( Ct + Cn ) =
( Ct + Cn ) x ( Ct + Cn ) =
Ct + Cn + Cqnt
+ Cqnn.
This result arises by way of two key rules of categorial algebra, plus the general rule for multiplication when one category-symbol is multiplied by a different category-symbol [we used a special case of this general rule, for the case where the same category-symbol is multiplied by itself, in step s = 1, above] --
1. general case: CqY x
CqX = CqX + CqYX = CX + CqYX;
special case: CqX x CqX = CqX + CqXX = CX + CqXX.
2. Cqx +
Cqx = Cqx; the same category-symbol, added to itself, does not
make “two” of that category-symbol; one “copy” of each category is sufficient;
two or more copies of any category would be redundant, for the purposes of this dialectical-categorial algebra.
3. There
is no Cqw
such that Cqx + Cqy = Cqw; different
category-symbols, added together [as opposed to being ‘‘‘multiplied’’’], do not
reduce to a single category-symbol, just like in the proverbial case of ‘apples + oranges’, or a + o.
Well, we already know how to
“solve-for” Cqnn.
It describes a category
“containing” two sub-categories, the first sub-category being one of ‘muLtiplications OF
muLtiplications’,
and the second sub-category being one of ‘diVisions OF
diVisions’.
The first sub-category is one each of whose
units / operations is a ‘muLtiplication OF
muLtiplications’,
i.e., each of which is a ‘meta-muLtiplication’, such that each such ‘meta-muLtiplication’
operation is made up out of a multiplicity of muLtiplication
operations.
Our experiences of / "in" the ‘basic
arithmetical operations’ domain suggest that such arithmetical operations do indeed
presently exist.
That sub-category-description
describes the sub-category of ‘multi-muLtiplication’ operations -- i.e., of “exPonentiations”: “exPonentiation” is a basic arithmetical operation which
is “made up out of multiple [repeated] muLtiplication operations, viz. --
23 = 2 xx 3 = 2 x 2 x 2 = 8 ≠ 9 = 3 x 3 = 3 xx 3 = 32.
I.e., “two cubed”, or “two
raised to the exponent three”, is “made of” a product involving three twos,
that yields eight, whereas “three squared”, or “three raised to the exponent
two”, yields nine: in general, the
order of “base” and “exponent” cannot be reversed without changing the result
as well.
Generally, each order will return a different result.
Generally, each order will return a different result.
The second sub-category should be, per our standard method, one each of whose units / operations is a ‘diVision OF diVisions’, i.e., each of which is a ‘meta-diVision’, such that each such ‘meta-diVision’ operation is made up out of a multiplicity of diVision operations.
That is, the second sub-category should be one of ‘multi-diVision’ operations, “made up out of multiple [repeated] diVision operations.
We interpret this to be the “inverse” operation of ‘de-exPonentiation’, or of “nth Root extraction”.
The “log” operation, which returns exponents, not bases or roots, is also a candidate for this “inverse” operation, but is not as fully this inverse operation as is the Root extraction operation.
Given our experience of / "in" the domain of ‘basic arithmetical operations’, this sub-category description may, at this point, give us pause.
Many of us may be unfamiliar with the algorithms by which the “nth” root(s) of a given number are “extracted”.
In what sense, if any, can an exponentiation be reversed, the “root” “extracted” from its “power”, by repeated division?
But let us consider the method of
extracting square roots that is perhaps the oldest such method still
known.
It is called “The Babylonian Method”, and also “Heron’s Method”, because the storied Heron of Ancient Alexandria is the most ancient source known to have written an explicit account of this method.
This method is, by the way, a special case of the more general “Newton’s Method”, but predates the discovery of “Newton’s Method” by many centuries.
The method involves guessing a “starting estimate” for the square root sought, followed by repeated stages of, well, diVision -- division of the square by the current best estimate of its square root -- followed by, well, diVision again -- this time division of the sum of the previous consecutive pair of estimates by two, thus averaging them -- to obtain the next better estimate of the square root, all leading to an improving estimate for the square root with each iteration of the ‘double diVision’ just described.
‘Formulaically’, the next better estimate of the square’s square root, xn+1, is derived from the previous best estimate, xn, by dividing the square, S, by the previous best estimate, xn, summing xn and S÷xn, then dividing that sum by 2:
xn+1 = ( xn + S÷xn ) ÷ 2.
It is called “The Babylonian Method”, and also “Heron’s Method”, because the storied Heron of Ancient Alexandria is the most ancient source known to have written an explicit account of this method.
This method is, by the way, a special case of the more general “Newton’s Method”, but predates the discovery of “Newton’s Method” by many centuries.
The method involves guessing a “starting estimate” for the square root sought, followed by repeated stages of, well, diVision -- division of the square by the current best estimate of its square root -- followed by, well, diVision again -- this time division of the sum of the previous consecutive pair of estimates by two, thus averaging them -- to obtain the next better estimate of the square root, all leading to an improving estimate for the square root with each iteration of the ‘double diVision’ just described.
‘Formulaically’, the next better estimate of the square’s square root, xn+1, is derived from the previous best estimate, xn, by dividing the square, S, by the previous best estimate, xn, summing xn and S÷xn, then dividing that sum by 2:
xn+1 = ( xn + S÷xn ) ÷ 2.
Let us apply this method to “extracting” the “square root” from the “square”, 9, with “starting estimate”
of x1 = 2 --
n....Current
Best Estimate ( xn )...DiVide
Square by That Estimate ( S÷xn )..DiVide
Their Sum by 2 for new est.
1....2..............................9÷2 = 4.5................................(2+4.5)÷2 = 3.25
2....3.25.......................9÷3.25 ≈ 2.769...................(3.25+2.769)÷2 ≈ 3.01
3....3.01.......................9÷3.01 ≈ 2.99......................(3.01+2.99)÷2 ≈ 3.000
4....3.000....................9÷3.000 = 3.000.................(3.000+3.000)÷2 = 3.000
After n =
3, with "rounding" as shown above, the method reaches a “fixed point” / “equilibrium”
at x3+... = 3, which is the positive square root of 9.
Thus we see in what sense, in this method at least, square root extraction is made up out of repeated diVisions.
at x3+... = 3, which is the positive square root of 9.
Thus we see in what sense, in this method at least, square root extraction is made up out of repeated diVisions.
We may thus “assert” our
solution as follows --
Cqnn =
Cqe = Ce = Cq[P + Ri] =
Cq[LL + VVi] [---) Cq[4 + 4i].
Cq[LL + VVi] [---) Cq[4 + 4i].
Our step s = 2 equation-model, as we have solved it so far, thus now looks like this --
C)-|-(2 = Ct2^2 =
Ct4 =
Ct + Cn + Cqnt + Ce
Ct + Cn + Cqnt + Ce
[---)
Cq[1 + 1i] + Cq[2 + 2i] + Cq[3 + 3i] + Cq[4 + 4i]
-- since we have not yet determined which actual category of the ‘basic arithmetic operations’ domain is described by the algorithmically-generated symbol Cqnt -- if any, i.e., if Cqnt is not an “empty category”, “inoperative” for this domain.
When, as a component of ( Ct + Cn ) x ( Ct + Cn ), the
“higher-complexity” category, Cn, operates upon / “multiplies” the “lower-complexity”
category, Ct --
Cn x Ct = Ct + Cqnt = Cq[A + Si] +
Cq[LA + VSi]
-- generically speaking, the categorial
relationship to be called to the user’s attention by this operation, in this
‘categorial arithmetic’, is, again, a synchronic
«aufheben»
relationship, this time, that between Ct and Cqnt.
It calls the user to search
that user’s knowledge and memory of the domain in question -- in this specific case, the domain
of ‘basic arithmetical operations’ -- for a category which represents an
“uplift” of category Ct entities to the level of the entities native to
category Cn, thereby “canceling” the Ct-type entities concerned, at their own native level, but, by the same
token, “preserving” those category Ct entities at the Cn level, combining Cn and Ct qualities,
in the relationship of “elevation” of those category Ct entities within the level typical of category Cn entities.
Thus, the additional category thereby presented, Cqnt, signifies a category whose units are the operational interactions of the Ct operations with the Cn operations, as codified in the axioms, and/or theorems, and/or corollaries, and/or lemmas, and/or ‘‘‘rules’’’ of the “Real Numbers” system of arithmetic.
Thus, the additional category thereby presented, Cqnt, signifies a category whose units are the operational interactions of the Ct operations with the Cn operations, as codified in the axioms, and/or theorems, and/or corollaries, and/or lemmas, and/or ‘‘‘rules’’’ of the “Real Numbers” system of arithmetic.
The first sub-category of the category Cqnt = Cq[LA + VSi] answers to a sub-category description which connotes
the way in which, or the ‘‘‘rules’’’ by which, the operation of muLtiplication “subsumes” the operation of Addition, denoted herein by ‘L | A’.
To our lights, this
sub-category-description connotes the “distributive law” of “Real” arithmetic, an axiom of that system of
arithmetic, which codifies the interaction of the addition operation with the
multiplication operation -- the rule that the multiplication operation
“distributes over” the addition operation. This “law” involves two components, often called “left
distributivity” and “right distributivity”, respectively --
·
[“left
distributivity”]: For all elements a, b, c of R,
c x (a + b) = (c x a) + (c x b).
c x (a + b) = (c x a) + (c x b).
·
[“right
distributivity”]: For
all elements a, b, c of R,
(a + b) x c = (a x c) + (b x c).
(a + b) x c = (a x c) + (b x c).
The second sub-category of the category Cqnt = Cq[LA + VSi] answers to a sub-category description which connotes
the ‘‘‘rules’’’ by which the operation of diVision “subsumes” the
operation of Subtraction, denoted ‘V | S’.
To our lights, this
sub-category-description connotes a “non-distributive rule” of “Real” arithmetic for ‘diVision / Subtraction’, although
this rule is, typically, not an explicit one in presentations and in
axiomatizations of “Real”
arithmetic. It is learned
informally, as a joint consequence of other rules, i.e., as [partly] already
subsumed under, or included in, the “distributive law”, or is encountered as a
theorem, corollary, or lemma.
First of all, note that diVision does not fully “distribute” over [ ‘|’ ] Addition:
·
[‘‘‘left non-distributivity’’’, ‘V | A’]: For some a, b, c of R, (a + b) ≠ 0,
c ÷ (a + b) ≠ (c ÷ a) + (c ÷ b).
c ÷ (a + b) ≠ (c ÷ a) + (c ÷ b).
·
[‘‘‘right
distributivity’’’, ‘V | A’]: For
all a, b, c of R, c ≠ 0,
(a + b) ÷ c = (a ÷ c) + (b ÷ c).
(a + b) ÷ c = (a ÷ c) + (b ÷ c).
The (a
+ b) ≠ 0 and c ≠ 0
proviso’s are necessary, in these assertions about ‘V | A’,
because diVisions by zero invoke a value that resides beyond the
‘‘‘number-space’’’of the set R.
But the second sub-category
of Cqnt = Cq[LA + VSi] pertains directly to the interaction of the diVision operation with the Subtraction operation, not with the Addition operation [although, given that the set R includes “signed numbers” with “negative” signs,
i.e., “additive inverses”, as well as the subtraction operation-sign, additions
can also express subtractions, i.e., if b
= -d,
then a + b = a - d], e.g.:
then a + b = a - d], e.g.:
·
[‘‘‘left non-distributivity’’’, ‘V | S’]: For some a, b, c of R,
(a - b) ≠ 0, c ÷ (a - b) ≠ (c
÷ a) - (c ÷ b)
-- e.g. --
3 ÷ (1 - 2 ) = -3 ≠ 1.5 = ( 3÷1) - (3÷2).
-- e.g. --
3 ÷ (1 - 2 ) = -3 ≠ 1.5 = ( 3÷1) - (3÷2).
·
[‘‘‘right
distributivity’’’, ‘V | S’]: For
all a, b, c of R, c ≠ 0,
(a - b) ÷ c = (a ÷ c) - (b ÷ c).
(a - b) ÷ c = (a ÷ c) - (b ÷ c).
If we re-express subtractions
as additions, and divisions as multiplications -- which the “Real” number arithmetic enables us to do, since it
includes ratios and “multiplicative inverses”, as well as “additive inverses”,
we see that the “Real”
arithmetic’s '''rules''' for ‘V | S’ are partly implicit in the ‘L | A’ '''rules''',
e.g., if we set b = -d and c = 1÷e = 1/e, e ≠ 0:
·
[an aspect of ‘L | A’]: For a,
-d, 1/e of R, (a + d) ≠ 0,
1/e x 1/(a + d) = 1/((e x a) + (e x b))
1/e x 1/(a + d) = 1/((e x a) + (e x b))
-- e.g. --
1/(1/3) x 1/(1 + -2 ) =
-3 =
1/( 1/3 x 1) + ( 1/3 x -2) ).
1/(1/3) x 1/(1 + -2 ) =
-3 =
1/( 1/3 x 1) + ( 1/3 x -2) ).
·
[‘‘‘right
distributivity’’’, ‘L | A’]: For
all a, -d, 1/e of R, e ≠ 0,
(a + d) x 1/e = (a x 1/e) + (d x 1/e),
(a + d) x 1/e = (a x 1/e) + (d x 1/e),
-- e.g. --
(1 + -2) x (1/(1/3)) =
-3 =
( 1 x (1/(1/3)) ) + ( -2 x (1/(1/3)) ).
(1 + -2) x (1/(1/3)) =
-3 =
( 1 x (1/(1/3)) ) + ( -2 x (1/(1/3)) ).
The subscript ‘VSi’ component of the subscript ‘[LA + VSi]’ of categopry-symbol --
Cq[LA + VSi] = Cqnt
-- can thus be interpreted as calling attention systematically and explicitly, if somewhat redundantly, to the specific ‘V | S’ rules, which differ from the generic ‘L | A’ rules, in that the ‘V | S’ rules require the making explicit of special restrictions [e.g, 0 denominators not allowed], etc., as we have seen above.
We may therefore write our full solution for step s = 2 as --
C)-|-(2 = Ct2^2 = Ct4 =
Ct + Cn + Cqnt + Ce
Ct + Cn + Cqnt + Ce
additions & subtractions +
multiplications & divisions +
n & t interactions +
multiplications & divisions +
n & t interactions +
exponentiations & de-exponentiations.
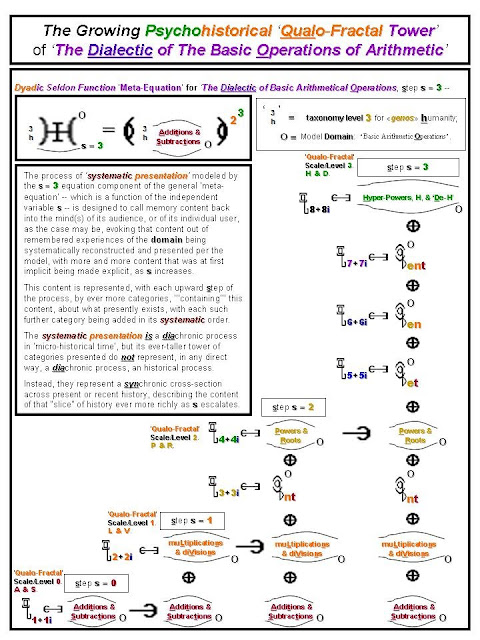
Our categorial progression so
far can be summarized textually as below.
The ‘qualo-fractal’
content-structure of this psychohistorical dialectic to step 2 can be summarized as follows --
exponentiations & de-exponentiations “contain” multiplications & divisions,
which, in turn, “contain” additions & subtractions.
The “five symbolic-elements
expression” for this model is thus Ct2^2 [five if we count the underscore under the t as a separate “symbolic-element”].
The systematic dialectic of
the basic operations of arithmetic ‘‘‘presently’’’ and “standardly” ends here,
at step s = 2,
with the category named exponentiations & de-exponentiations
as its ‘meta-meristemal’ category, or
‘‘‘vanguard’’’ category.
We like the compactness of
the CQ_ representation
of this systematic dialectic, whose “final step” can be modeled via a single equation --
C)-|-(2 = Ct + Cn + Cqnt
+ Ce.
However, there is also the
alternative of expressing each step of this
dialectic by two separate equations,
using the NQ_ dialectical algebra instead, e.g. --
verse)-|-(2 = CA + CL + CqLA
+ CP,
for the ‘‘‘verse’’’ operations.
for the ‘‘‘verse’’’ operations.
inverse)-|-(2 = CS + CV + CqVS
+ CR,
for the ‘‘‘inverse’’’, or ‘‘‘reverse’’’, operations.
for the ‘‘‘inverse’’’, or ‘‘‘reverse’’’, operations.
Stage 3. To
iterate our CQ_ ‘meta-equation’,
C)-|-(s = Ct2^s = ( Cq[A + Si] )2^s,
for step s = 3, is to iterate the systematic presentation of the domain of basic arithmetical operations beyond the “basic”, beyond the “present”, beyond the conventional conclusion of that presentation, and beyond the “systematic reconstruction” of this domain at present, to a somewhat “preconstructive” -- somewhat “predictive” -- extrapolation of its possible future. However, as we shall see, we have already encountered units of the “vanguard” term of step s = 3, in this very text.
C)-|-(s = Ct2^s = ( Cq[A + Si] )2^s,
for step s = 3, is to iterate the systematic presentation of the domain of basic arithmetical operations beyond the “basic”, beyond the “present”, beyond the conventional conclusion of that presentation, and beyond the “systematic reconstruction” of this domain at present, to a somewhat “preconstructive” -- somewhat “predictive” -- extrapolation of its possible future. However, as we shall see, we have already encountered units of the “vanguard” term of step s = 3, in this very text.
Let’s see what are the
additional category-descriptions that this step s = 3 ‘self-iteration’ generates:
C)-|-(3 = Ct2^3
= Ct8 =
( Ct4 )2 =
(Ct + Cn + Cqnt + Ce )2 =
(Ct + Cn + Cqnt + Ce )2 =
(Ct + Cn + Cqnt + Ce ) x (Ct + Cn + Cqnt + Ce ) =
Ct + Cn + Cqnt + Ce +
Cqet + Cqen + Cqent + Cqee
[---)
Cq[1 + 1i] + Cq[2 + 2i] + Cq[3 + 3i] + Cq[4 + 4i] +
Cq[5 + 5i] + Cq[6 + 6i] + Cq[7 + 7i]
+ Cq[8 + 8i].
We know -- from past experience, narrated above -- how to “solve-for”category
Cqee = Cq[PP + RRi].
It describes a category
“containing” two sub-categories, the first sub-category being one of ‘Powers OF
Powers’,
and the second sub-category being one of ‘Root-extractions OF
Root-extractions’.
The first sub-category is one each of whose
units / operations is an ‘exPonentiation OF
exPonentiations’,
i.e., each of which is a ‘meta-exPonentiation’, such that each such ‘meta-exPonentiation’
operation is made up out of a multiplicity of exPonentiation
operations.
But that is precisely the new operation that we have encountered in this text, at the heart of the Seldon Functions in general, and at the heart of our CQ_ ‘meta-equation’ --
C)-|-(s = Ct2^s
-- specifically.
A unit increment in the
‘meta-exponent’ of the ‘starting-category’ symbol of that ‘meta-equation’,
corresponding to a unit increment in its step-value, s, is equivalent to a two-fold exponentiation of that ‘starting-category’ symbol. e.g.
--
Ct2
= Ct2^1;
(Ct2 )2 = (Ct2^1 )2 = (Ct2^1 )2^1 = Ct2^(1+1) = Ct2^2
(Ct2 )2 = (Ct2^1 )2 = (Ct2^1 )2^1 = Ct2^(1+1) = Ct2^2
-- because repeated exponents
mutually multiply,
and because 'meta-exponents' of exponents add
together when those 'meta-exponents' have the same exponents as their bases, and
are multiplied together.
Let’s call this sub-category Hyper-exponentiation, or H for short.
The second sub-category should be for operations which are ‘de-exponentiations OF de-exponentiations’, i.e., which are ‘meta-de-exponentiations’, such that each ‘meta-de-exponentiation’ operation is made up out of a multiplicity of de-exponentiation operations.
Let’s call this sub-category Hyper-exponentiation, or H for short.
The second sub-category should be for operations which are ‘de-exponentiations OF de-exponentiations’, i.e., which are ‘meta-de-exponentiations’, such that each ‘meta-de-exponentiation’ operation is made up out of a multiplicity of de-exponentiation operations.
That is, the second sub-category
should be one of ‘multi-de-exponentiation’ operations, “made up out of multiple [repeated] de-exponentiation operations, each denoted by '√', the sign of the "square-root"-extracting operation.
We can use the ‘self-example’, exemplified in this very text, to illustrate this process:
We can use the ‘self-example’, exemplified in this very text, to illustrate this process:
√√√Ct +Cn +Cqnt+Ce +Cqet+Cqen+Cqent+Cqee =
√√√Ct2^3 =
√√Ct + Cn + Cqnt + Ce =
√√Ct2^2 =
√√√Ct2^3 =
√√Ct + Cn + Cqnt + Ce =
√√Ct2^2 =
_____________
√ Ct + Cn =
√Ct2^1 =
Ct2^(3-3) =
Ct2^0 =
Ct.
Let’s call this sub-category De-Hyper-exponentiation, or D for short.
√Ct2^1 =
Ct2^(3-3) =
Ct2^0 =
Ct.
Let’s call this sub-category De-Hyper-exponentiation, or D for short.
We may thus “assert” our solution
as follows --
Cqee = Cqm = Cm = Cq[H + Di] [---) Cq[8 + 8i].
Cqee = Cqm = Cm = Cq[H + Di] [---) Cq[8 + 8i].
Our step s = 3 equation-model, as we have solved it so far, thus now looks like this --
C)-|-(3 = Ct2^3
= Ct8 =
Ct + Cn + Cqnt + Ce + Cqet + Cqen + Cqent + Cm
Ct + Cn + Cqnt + Ce + Cqet + Cqen + Cqent + Cm
-- since we have not yet
determined which actual categories of the ‘basic arithmetical operations’
domain are described by the algorithmically-generated ‘category-description’
symbols Cqet, Cqen, and Cqent, if any.
But we already know how to
characterize the possible
categories that these three category-symbols “call for”, viz. --
· Cqet [---) Cq[5 + 5i] “calls for” a '''hybrid''' category for the kind of ‘meta-operation’, or ‘operation of operations’,
that combines the e and t operations.
that combines the e and t operations.
· Cqen [---) Cq[6 + 6i] “calls for” a '''hybrid''' category for the kind of ‘meta-operation’, or ‘operation of
operations’, that combines the e and n operations.
operations’, that combines the e and n operations.
· Cqent [---) Cq[7 + 7i] “calls for” a '''hybrid''' category for the kind of ‘meta-operation’, or ‘operation of
operations’, that combines the e and the Cqnt.
operations’, that combines the e and the Cqnt.
We may thus write our full solution for step s = 3 as --
C)-|-(3 = Ct2^3
=
Ct8 =
Ct + Cn + Cqnt + Ce + Cqet + Cqen + Cqent + Cm =
Ct + Cn + Cqnt + Ce + Cqet + Cqen + Cqent + Cm =
additions & subtractions +
multiplications & divisions +
n with t interactions +
multiplications & divisions +
n with t interactions +
exponentiations & de-exponentiations +
e with t interactions +
e with n interactions +
e with n & t interactions +
meta-exponentiations & de-meta-exponentiations.
Our categorial progression so far can be summarized textually as below.
The ‘qualo-fractal’ content-structure of this psychohistorical dialectic through step 3 can be summarized as follows --
meta-exponentiations & de-meta-exponentiations “contain”
exponentiations & de-exponentiations, which “contain”
multiplications & divisions, which “contain”
additions & subtractions.
The “five symbolic-elements
expression” for this model, up to this step, is thus Ct2^3.


No comments:
Post a Comment